Please find the important C-programs which shall be encountered in interviews and let me know if there is any incorrect info.
I have tried to display the efficient algorithm for the given problem.
1] How to find out the Maximum number in a array?
#include<stdio.h>
int main()
{
int a[20] = {0}, i, n, BIG;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Intialise the BIG variable to a[0] */
BIG = a[0];
for(i=1; i<n; i++)
{
if(BIG < a[i])
BIG = a[i];
}
printf(" The value of MAX Number in array is :%d\n", BIG);
}
2] How to find out the Minimum number in a array?
#include<stdio.h>
int main()
{
int a[20] = {0}, i, n, SMALL;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Intialise the SMALL variable to a[0] */
SMALL = a[0];
for(i=1; i<n; i++)
{
if(SMALL > a[i])
SMALL = a[i];
}
printf(" The value of MIN Number in array is :%d\n", SMALL);
}
(or) One more logic can be used to find out MIN number in a array !!!
#include<stdio.h>
int main()
{
int a[20] = {0}, i, n, SMALL;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Intialise the SMALL variable to 0 */
SMALL = 0;
for(i=1; i<n; i++)
{
if(a[SMALL] > a[i])
SMALL = i;
}
printf(" The value of MIN Number in array is :%d\n", a[SMALL]);
}
3] How to find out the second Minimum number in a array?
There are several ways to find out the second minimum number.
1. using Bubble sort sort the elements in to ascending order and find out the minimum value and its complexity is O(n^2)
2. There is other way of implementing with complexity of O(n), please find the same below.
#include<stdio.h>
int main()
{
int a[20] = {0}, i, n, first, second;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* 1. Intialise the SMALL variable to 0 */
first = second = 32767 /* INT_MAX VALUE */;
for(i=0; i<n; i++)
{
/* If the current number is less than first
then update first and second */
if (a[i] < first)
{
second = first;
first = a[i];
}
/* If the current number is in between first and second
then update second */
else
{
if((a[i] < second) && (a[i] != first))
{
second = a[i];
}
}
}
if(second == 32767)
{
printf(" There is no second element \n");
}
else
{
printf(" The value of first :%d second: %d\n", first, second);
}
}
==================================
What is sorting?
Sorting means arranging elements in a particular order (Ascending /Descending Order).
There are many factors to be considered before choosing best algorithm.
1. Time complexity -> How much time does the algorithm take to complete.
2. Space complexity -> how much working memory (typically RAM) is needed by the algorithm. This has two aspects: the amount of memory needed by the code, and the amount of memory needed for the data on which the code operates. Choose the best sorting algorithm based on the complexity,
complexity generally represents in BIG-O-Notation O(n), O(n^2) etc..
1] Bubble Sort Algorithm :(Ascending Order) (O(n^2))
This is the simple Algorithm. Best and worst case case time complexity of this algorithm O(n^2). This algorithm can be improved and achieve best case complexity as O(n).
#include<stdio.h>
int main()
{
int a[20] = {0}, i, j, temp, n;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Ist Loop (Main Loop) */
for(i=0; i<n; i++)
{
/* Second Loop */
for(j=0; j<n-i-1; j++)
{
if(a[j] > a[j+1])
{
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
}
}
for(i=0; i<n; i++)
{
printf(" The value of a[%d]: %d\n", i, a[i]);
}
}
1] Improved Bubble Sort Algorithm :(Ascending Order) (O(n))
#include<stdio.h>
int main()
{
int a[20] = {0}, i, j, temp, n, swapped;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
swapped = 1;
/* Ist Loop (Main Loop) */
/*
for(i=0; ((i<n) && (swapped)); i++)
/* Second Loop */
for(j=0; j<n-i-1; j++)
{
if(a[j] > a[j+1])
{
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
/
swapped = 1;
}
}
}
for(i=0; i<n; i++)
{
printf(" The value of a[%d]: %d\n", i, a[i]);
}
}
2] Selection Sort Algorithm :(Ascending Order) (O(n^2))
#include<stdio.h>
int main()
{
int a[20] = {0}, i, j, temp, n, index_min;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Step 1: */
/* find out the Min Index */
/* Ist Loop (Main Loop) */
for(i=0; i<n; i++)
{
/* Finding the min value */
index_min = i;
/* Second Loop */
for(j=i; j<n; j++)
{
if(a[index_min] > a[j])
index_min = j;
}
/* swap the values */
temp = a[i];
a[i] = a[index_min];
a[index_min] = temp;
}
for(i=0; i<n; i++)
{
printf(" The value of a[%d]: %d\n", i, a[i]);
}
}
2] Quick sort Algorithm :(Ascending Order) (O(n log n))
Quick sort is a divide and conquer algorithm.
It has two phases 1. partition phase 2. Sorting phase
pivot_item = partition(array, low, high) -> O(n)
quick_sort(a, low, pivot-1) -> T(n/2)
quick_sort(a, pivot+1, high) -> T(n/2) => O(n)+ T(n/2)+T(n/2) = O(n log n)
Given an array of n elements (e.g., integers):
If array only contains one element, return
Else
pick one element to use as pivot.
Partition elements into two sub-arrays:
Elements less than or equal to pivot
Elements greater than pivot
Quicksort two sub-arrays
Return results
#include<stdio.h>
/*
* partition_array()
*/
int partition_array(int a[], int low, int high)
{
int pivot, left, right, temp;
left = low;
right = high;
pivot = a[low];
while(left < right)
{
// Move left while item < pivot
while(a[left]<= pivot)
{
left++;
}
// Move right while item > pivot
while(a[right] > pivot)
{
right--;
}
if(left < right)
{
temp = a[left];
a[left] = a[right];
a[right]= temp;
}
}
// right is final position for the pivot
a[low] = a[right];
a[right] = pivot;
return right;
}
/*
* Quick Sort
*/
void quicksort(int a[], int low, int high)
{
int pivot_item;
// Termination
if(high > low)
{
pivot_item = partition_array(a, low, high);
printf("pivot_item :%d\n", pivot_item);
/* Left side sort the Elements. Traverse before Pivot_item */
quicksort(a, low, pivot_item-1);
/* Right side sort the Elements Traverse After Pivot_item */
quicksort(a, pivot_item+1, high);
}
}
int main()
{
int a[20] = {0}, i, j, temp, n, index_min;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Step 1: */
/* Find out the pivot element using Partition */
/* Sort the elements using recursion */
quicksort(a, 0, n-1);
for(i=0; i<n; i++)
{
printf(" The value of a[%d]: %d\n", i, a[i]);
}
}
For better animation, please check this interactive tutorial.
http://people.stern.nyu.edu/panos/java/Quicksort/index.html
3] Merge sort Algorithm :(Ascending Order) (O(n log n))
Merge sort is based on divide and conquer algorithm.
The mergesort algorithm is as follows; its execution is illustrated as following:
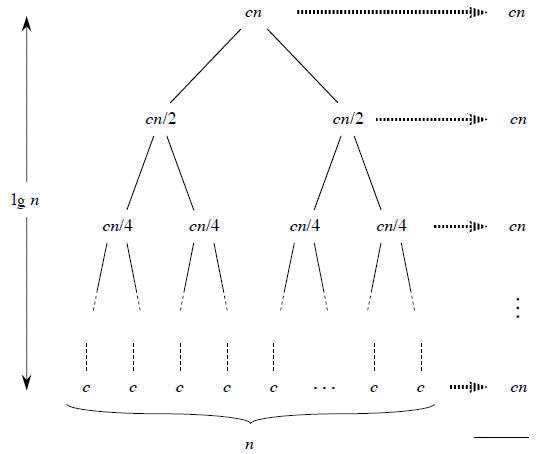 -> cn lg n + cn.
-> cn lg n + cn.
ignoring low-order term of cn and constant coeffcient c, and we have,
I have tried to display the efficient algorithm for the given problem.
1] How to find out the Maximum number in a array?
#include<stdio.h>
int main()
{
int a[20] = {0}, i, n, BIG;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Intialise the BIG variable to a[0] */
BIG = a[0];
for(i=1; i<n; i++)
{
if(BIG < a[i])
BIG = a[i];
}
printf(" The value of MAX Number in array is :%d\n", BIG);
}
2] How to find out the Minimum number in a array?
#include<stdio.h>
int main()
{
int a[20] = {0}, i, n, SMALL;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Intialise the SMALL variable to a[0] */
SMALL = a[0];
for(i=1; i<n; i++)
{
if(SMALL > a[i])
SMALL = a[i];
}
printf(" The value of MIN Number in array is :%d\n", SMALL);
}
(or) One more logic can be used to find out MIN number in a array !!!
#include<stdio.h>
int main()
{
int a[20] = {0}, i, n, SMALL;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Intialise the SMALL variable to 0 */
SMALL = 0;
for(i=1; i<n; i++)
{
if(a[SMALL] > a[i])
SMALL = i;
}
printf(" The value of MIN Number in array is :%d\n", a[SMALL]);
}
3] How to find out the second Minimum number in a array?
There are several ways to find out the second minimum number.
1. using Bubble sort sort the elements in to ascending order and find out the minimum value and its complexity is O(n^2)
2. There is other way of implementing with complexity of O(n), please find the same below.
#include<stdio.h>
int main()
{
int a[20] = {0}, i, n, first, second;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* 1. Intialise the SMALL variable to 0 */
first = second = 32767 /* INT_MAX VALUE */;
for(i=0; i<n; i++)
{
/* If the current number is less than first
then update first and second */
if (a[i] < first)
{
second = first;
first = a[i];
}
/* If the current number is in between first and second
then update second */
else
{
if((a[i] < second) && (a[i] != first))
{
second = a[i];
}
}
}
if(second == 32767)
{
printf(" There is no second element \n");
}
else
{
printf(" The value of first :%d second: %d\n", first, second);
}
}
==================================
SORTING
===================================================
What is sorting?
Sorting means arranging elements in a particular order (Ascending /Descending Order).
There are many factors to be considered before choosing best algorithm.
1. Time complexity -> How much time does the algorithm take to complete.
2. Space complexity -> how much working memory (typically RAM) is needed by the algorithm. This has two aspects: the amount of memory needed by the code, and the amount of memory needed for the data on which the code operates. Choose the best sorting algorithm based on the complexity,
complexity generally represents in BIG-O-Notation O(n), O(n^2) etc..
1] Bubble Sort Algorithm :(Ascending Order) (O(n^2))
This is the simple Algorithm. Best and worst case case time complexity of this algorithm O(n^2). This algorithm can be improved and achieve best case complexity as O(n).
#include<stdio.h>
int main()
{
int a[20] = {0}, i, j, temp, n;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Ist Loop (Main Loop) */
for(i=0; i<n; i++)
{
/* Second Loop */
for(j=0; j<n-i-1; j++)
{
if(a[j] > a[j+1])
{
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
}
}
for(i=0; i<n; i++)
{
printf(" The value of a[%d]: %d\n", i, a[i]);
}
}
1] Improved Bubble Sort Algorithm :(Ascending Order) (O(n))
#include<stdio.h>
int main()
{
int a[20] = {0}, i, j, temp, n, swapped;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
swapped = 1;
// set swapped to 1 to start first pass/* Ist Loop (Main Loop) */
/*
if flag becomes 0 then sorting stops */for(i=0; ((i<n) && (swapped)); i++)
{/* Second Loop */
for(j=0; j<n-i-1; j++)
{
if(a[j] > a[j+1])
{
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
/
* It indicates that a swap occurred. */ swapped = 1;
}
}
}
for(i=0; i<n; i++)
{
printf(" The value of a[%d]: %d\n", i, a[i]);
}
}
2] Selection Sort Algorithm :(Ascending Order) (O(n^2))
This algorithm is simple and not efficient than insertion sort and it proceeds by finding the smallest (or largest, depending on
sorting order) element in the unsorted sublist, exchanging it with the
leftmost unsorted element (putting it in sorted order), and moving the
sublist boundaries one element to the right.
#include<stdio.h>
int main()
{
int a[20] = {0}, i, j, temp, n, index_min;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Step 1: */
/* find out the Min Index */
/* Ist Loop (Main Loop) */
for(i=0; i<n; i++)
{
/* Finding the min value */
index_min = i;
/* Second Loop */
for(j=i; j<n; j++)
{
if(a[index_min] > a[j])
index_min = j;
}
/* swap the values */
temp = a[i];
a[i] = a[index_min];
a[index_min] = temp;
}
for(i=0; i<n; i++)
{
printf(" The value of a[%d]: %d\n", i, a[i]);
}
}
2] Quick sort Algorithm :(Ascending Order) (O(n log n))
Quick sort is a divide and conquer algorithm.
It has two phases 1. partition phase 2. Sorting phase
pivot_item = partition(array, low, high) -> O(n)
quick_sort(a, low, pivot-1) -> T(n/2)
quick_sort(a, pivot+1, high) -> T(n/2) => O(n)+ T(n/2)+T(n/2) = O(n log n)
Given an array of n elements (e.g., integers):
If array only contains one element, return
Else
pick one element to use as pivot.
Partition elements into two sub-arrays:
Elements less than or equal to pivot
Elements greater than pivot
Quicksort two sub-arrays
Return results
#include<stdio.h>
/*
* partition_array()
*/
int partition_array(int a[], int low, int high)
{
int pivot, left, right, temp;
left = low;
right = high;
pivot = a[low];
while(left < right)
{
// Move left while item < pivot
while(a[left]<= pivot)
{
left++;
}
// Move right while item > pivot
while(a[right] > pivot)
{
right--;
}
if(left < right)
{
temp = a[left];
a[left] = a[right];
a[right]= temp;
}
}
// right is final position for the pivot
a[low] = a[right];
a[right] = pivot;
return right;
}
/*
* Quick Sort
*/
void quicksort(int a[], int low, int high)
{
int pivot_item;
// Termination
if(high > low)
{
pivot_item = partition_array(a, low, high);
printf("pivot_item :%d\n", pivot_item);
/* Left side sort the Elements. Traverse before Pivot_item */
quicksort(a, low, pivot_item-1);
/* Right side sort the Elements Traverse After Pivot_item */
quicksort(a, pivot_item+1, high);
}
}
int main()
{
int a[20] = {0}, i, j, temp, n, index_min;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Step 1: */
/* Find out the pivot element using Partition */
/* Sort the elements using recursion */
quicksort(a, 0, n-1);
for(i=0; i<n; i++)
{
printf(" The value of a[%d]: %d\n", i, a[i]);
}
}
For better animation, please check this interactive tutorial.
http://people.stern.nyu.edu/panos/java/Quicksort/index.html
3] Merge sort Algorithm :(Ascending Order) (O(n log n))
Merge sort is based on divide and conquer algorithm.
The mergesort algorithm is as follows; its execution is illustrated as following:
- If the input sequence has only one element, return.
- Partition the input sequence into two halves.
- Sort the two subsequences using the same algorithm.
- Merge the two sorted subsequences to form the output sequence
- MERGE-SORT (Array, low, high)
1. IF low < high // Check for base case
2. THEN mid = (low + high)/2] // Divide step
3. MERGE-SORT (Array, low, mid) // Conquer step.
4. MERGE-SORT (Array, mid+ 1, high) // Conquer step.
5. MERGE (Array, low, mid, high) // Combine step.
 -> cn lg n + cn.
-> cn lg n + cn.ignoring low-order term of cn and constant coeffcient c, and we have,
Θ(n lg
n)
#include<stdio.h>
/*
* merge_sorted_arrays()
*/
int merge_sorted_arrays(int a[], int low, int mid, int high)
{
int i = low; /* Track first array */
int j = mid+1; /* Track second array */
int index = 0; /* Track temp array */
/* Temporary array is required */
int temp[50], k;
while((i<=mid) && (j<= high))
{
if(a[i] <= a[j])
{
temp[index] = a[i];
i++;
}
else
{
temp[index] = a[j];
j++;
}
index++;
}
while(i<=mid)
{
temp[index] = a[i];
index++;
i++;
}
while(j<=high)
{
temp[index] = a[j];
index++;
j++;
}
// Copy the temp array in to main Array
for(k=0; k<index; k++)
{
a[k+low] = temp[k];
}
}
/*
* Merge Sort -> Parition array using recursion
*/
void partition_array(int a[], int low, int high)
{
int mid;
// Termination
if(low < high)
{
mid = (low + high)/2;
/* Divide the Array till Mid */
partition_array(a, low, mid);
/* Divide the array from mid+1 */
partition_array(a, mid+1, high);
/* Combine the two sorted arrays in to one array. */
merge_sorted_arrays(a, low, mid, high);
}
}
/*
* Main()
*/
int main()
{
int a[20] = {0}, i, j, n;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Merge Sort */
partition_array(a, 0, n-1);
for(i=0; i<n; i++)
{
printf(" The value of a[%d]: %d\n", i, a[i]);
}
}
For Animation of Merge Sort: http://littlesnailworkshop.blogspot.in/2012/07/technique-merge-sort-animation.html
/*
* merge_sorted_arrays()
*/
int merge_sorted_arrays(int a[], int low, int mid, int high)
{
int i = low; /* Track first array */
int j = mid+1; /* Track second array */
int index = 0; /* Track temp array */
/* Temporary array is required */
int temp[50], k;
while((i<=mid) && (j<= high))
{
if(a[i] <= a[j])
{
temp[index] = a[i];
i++;
}
else
{
temp[index] = a[j];
j++;
}
index++;
}
while(i<=mid)
{
temp[index] = a[i];
index++;
i++;
}
while(j<=high)
{
temp[index] = a[j];
index++;
j++;
}
// Copy the temp array in to main Array
for(k=0; k<index; k++)
{
a[k+low] = temp[k];
}
}
/*
* Merge Sort -> Parition array using recursion
*/
void partition_array(int a[], int low, int high)
{
int mid;
// Termination
if(low < high)
{
mid = (low + high)/2;
/* Divide the Array till Mid */
partition_array(a, low, mid);
/* Divide the array from mid+1 */
partition_array(a, mid+1, high);
/* Combine the two sorted arrays in to one array. */
merge_sorted_arrays(a, low, mid, high);
}
}
/*
* Main()
*/
int main()
{
int a[20] = {0}, i, j, n;
printf("Enter the Array Size\n");
scanf("%d", &n);
printf("Enter the Array Elements\n");
for(i=0; i<n; i++)
scanf("%d", &a[i]);
/* Merge Sort */
partition_array(a, 0, n-1);
for(i=0; i<n; i++)
{
printf(" The value of a[%d]: %d\n", i, a[i]);
}
}
For Animation of Merge Sort: http://littlesnailworkshop.blogspot.in/2012/07/technique-merge-sort-animation.html